In order for the wavefunction and its first derivative to be continuous at
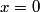 , we must have that , we must have that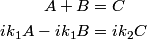 Solving for 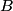 in terms of in terms of 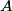 gives gives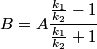 So, the reflection coefficient is 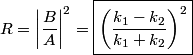 Therefore, answer (D) is correct. |
In order for the wavefunction and its first derivative to be continuous at
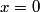 , we must have that , we must have that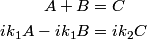 Solving for 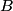 in terms of in terms of 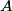 gives gives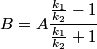 So, the reflection coefficient is 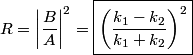 Therefore, answer (D) is correct. |